퍼셉트론_설명 (단층 퍼셉트론_SLP , 다층 퍼셉트론_MLP)
목차
- 퍼셉트론
- 단층 퍼셉트론
- 다층 퍼셉트론
1. 퍼셉트론

퍼셉트론은 인간의 뉴런 동작을 흉내낸 개념으로 일정치 이상의 크기를 가지면 출삭돌기를 통해 신호를 전달한다.


수식으로 살펴보면, x : 입력값, w: 가중치, y: 출력 으로 (x1*w1 + x2*w2 + x3*w3 + ... + xn*wn) 의 값이
임계치(threshold) 보다 크면 출력값이 1,
임계치(threshold) 보다 작으면 출력값이 0 이다.
이러한 함수를 계단 함수(Step function)라고 하며, 아래는 위의 수식을 나타낸 그래프이다.

(x1*w1 + x2*w2 + x3*w3 + ... + xn*wn) < θ(임계치) : y(출력값)=0
(x1*w1 + x2*w2 + x3*w3 + ... + xn*wn) >= θ(임계치) : y(출력값)=1

위의 식에서 임계치를 좌변으로 넘기고 편향 b (bias)로 표현할 수도 있습니다. 편향 b 또한 퍼셉트론의 입력으로 사용됩니다. 보통 그림으로 표현할 때는 입력값이 1로 고정되고 편향 b가 곱해지는 변수로 표현됩니다.
(x1*w1 + x2*w2 + x3*w3 + ... + xn*wn) + b < 0 : y(출력값)=0
(x1*w1 + x2*w2 + x3*w3 + ... + xn*wn) + b >= 0 : y(출력값)=1
2. 단층 퍼셉트론
윗 단계에서 배운 퍼셉트론은 단층 퍼셉트론이다. 퍼셉트론에는 2가지 종류가 있는데, 단층퍼셉트론과 다층퍼셉트론이다.
단층 퍼셉트론은 보내는 단계화 출력하는 두 단계로만 이루어 진다. 이때 각 단계를 layer 라 하고, x 는 입력층(input layer) y 는 출력층(output layer)이라 한다.

이 단층 퍼셉트론을 이용하면 AND, NAND, OR 게이트가 구현가능하다.
1. AND 게이트

def AND_gate(x1, x2):
w1 = 0.5
w2 = 0.5
b = -0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1AND_gate(0, 0), AND_gate(0, 1), AND_gate(1, 0), AND_gate(1, 1)(0, 0, 0, 1)
2. NAND 게이트
def AND_gate(x1, x2):
w1 = 0.5
w2 = 0.5
b = -0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1NAND_gate(0, 0), NAND_gate(0, 1), NAND_gate(1, 0), NAND_gate(1, 1)(1, 1, 1, 0)3. OR 게이트

def OR_gate(x1, x2):
w1 = 0.6
w2 = 0.6
b = -0.5
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1OR_gate(0, 0), OR_gate(0, 1), OR_gate(1, 0), OR_gate(1, 1)(0, 1, 1, 1)이처럼 단층 퍼셉트론은 AND,NAND,OR 게이트를 구현할 수 있지만 XOR 게이트는 구현이 불가능하다.
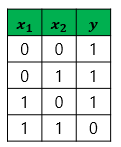
XOR 게이트는 입력값 두 개가 서로 다른 값을 갖고 있을때에만 출력값이 1이 되고, 입력값 두 개가 서로 같은 값을 가지면 출력값이 0이 되는 게이트이다. 위의 파이썬 코드에 아무리 수많은 가중치와 편향을 넣어봐도 XOR 게이트를 구현하는 것은 불가능하다. 그 이유는 단층 퍼셉트론은 직선 하나로 두 영역을 나눌 수 있는 문제에 대해서만 구현이 가능하기 때문입니다.
다음은 AND, NAND, OR 게이트를 그래프로 시각화 한 것이다.


그렇다면 XOR 게이트를 시각화 하면 어떻게 될까?
XOR 게이트는 입력값 두 개가 서로 다른 값을 갖고 있을때에만 출력값이 1이 되고, 입력값 두 개가 서로 같은 값을 가지면 출력값이 0이 되는 게이트이다. XOR 게이트를 시각화해보면 다음과 같다.

하얀색 원과 검은색 원을 직선 하나로 나누는 것은 불가능하므로 하나의 선만 생성이 가능한 단층 퍼셉트론으로는 XOR 게이트를 구현할 수 없다. 위의 좌측 그림과 같이 적어도 두 개의 선이 필요하다.
이에 대한 해답은 다층 퍼셉트론이다. 다층 퍼셉트론을 사용하면 2개의 선으로 분류할 수 있게 된다.
이는 은닉층을 2개이상으로 쌓으면 곡선으로도 분류 할 수 있는 DNN 이 된다.
3. 다층 퍼셉트론(MLP)
XOR 게이트는 층을 더 쌓으면 만들 수 있다. 단층 퍼셉트론의 차이는 단층 퍼셉트론은 입력층과 출력층만 존재하지만, 다층 퍼셉트론은 중간에 층을 더 추가하였다는 점이다. 이렇게 입력층과 출력층 사이에 존재하는 층을 은닉층(hidden layer)이라고 한다. 즉, 다층 퍼셉트론은 중간에 은닉층이 존재한다는 점이 단층 퍼셉트론과 다르다.
단층 퍼셉트론: 입력층 + 출력층
다층 퍼셉트론: 입력층 + 은닉층 + 출력층

이때, 은닉층의 개수는 여러개일 수 있다. 밑에는 은닉층이 2개인 경우이다.
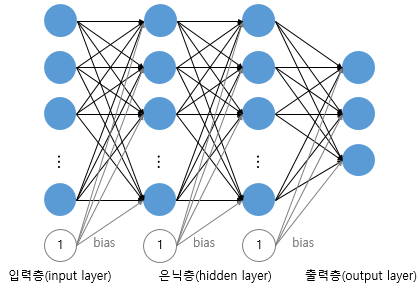
위와 같이 은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Network, DNN) 이라고 한다.
XOR 게이트

def AND_gate(x1, x2):
w1 = 0.5
w2 = 0.5
b = -0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
def NAND_gate(x1, x2):
w1 = -0.5
w2 = -0.5
b = 0.7
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
def OR_gate(x1, x2):
w1 = 0.6
w2 = 0.6
b = -0.5
result = x1*w1 + x2*w2 + b
if result <= 0:
return 0
else:
return 1
def XOR_gate(x1,x2):
s1=NAND_gate(x1,x2)
s2=OR_gate(x1,x2)
y=AND_gate(s1,s2)
return yXOR_gate(0,0), XOR_gate(0,1), XOR_gate(1,0), XOR_gate(1,1)(0,1,1,0)
